§ 5. Мноствы

5.1. Паняцце мноства

Разгледзім выказванне «Усе навучэнцы нашага класа маюць дома камп’ютар». Праўдзівае яно ці непраўдзівае? Для адказу на гэта пытанне вам трэба ў кожнага з аднакласнікаў удакладніць: «У цябе дома ёсць камп’ютар?» Калі ўсе навучэнцы класа адкажуць сцвярджальна, то выказванне праўдзівае, калі хоць бы адзін з навучэнцаў адкажа «няма»,
то і выказванне будзе непраўдзівым. Для розных класаў гэта выказванне будзе мець розныя значэнні, таму што рознымі будуць мноствы навучэнцаў класа.

Мноства — сукупнасць якіх-небудзь аб’ектаў, што валодаюць агульнай уласцівасцю. Гэтыя аб’екты называюць элементамі мноства.

Можна гаварыць пра мноства навучэнцаў 7 А класа, мноства адзнак у класным журнале, мноства гарадоў Беларусі, мноства літар рускага алфавіта і г. д. Паняцце мноства з’яўляецца адным з асноўных у матэматыцы.

Мноствы, як правіла, абазначаюць вялікімі лацінскімі літарамі, а элементы мностваў — маленькімі. Нагадаем, што для абазначэння прыналежнасці элемента мноству выкарыстоўваюць спецыяльныя знакі:

а ∈ М (элемент а належыць мноству М), а  ∉ М (элемент а не належыць мноству М). Калі мноства M складаецца з элементаў a, b, c, то гэта запісваюць так: M = {a, b, c}.

Каб задаць мноства, неабходна пералічыць яго элементы (прыклад 5.1) або назваць іх агульную ўласцівасць (прыклад 5.2).

5.2. Паняцце падмноства

Разгледзім мноства навучэнцаў якога-небудзь класа. У гэтым мностве можна вылучыць не толькі асобнага навучэнца, але і некаторыя групы навучэнцаў: выдатнікі; навучэнцы, што ўмеюць гуляць у тэніс, і г. д. Кожная з такіх груп утварае падмноства — частку мноства навучэнцаў.

Калі мноства А з’яўляецца падмноствам мноства М, то гэта запісваюць так: А ⊂ М. Запіс А ⊄ М абазначае, што мноства А не з’яўляецца падмноствам мноства М.

Падмноства можа змяшчаць усе элементы мноства, а можа не змяшчаць ніводнага (пустое мноства абазначаецца знакам ∅).

Некаторыя элементы мноства могуць належаць адначасова розным падмноствам (прыклад 5.3).

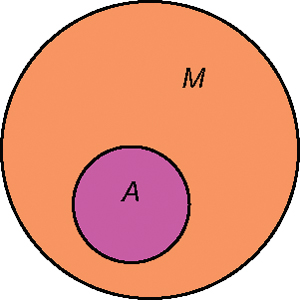
Для нагляднай геаметрычнай ілюстрацыі мностваў і адносін паміж імі выкарыстоўваюць кругі Эйлера. Кожнае мноства адлюстроўваецца кругам. Калі якое-небудзь мноства з’яўляецца падмноствам іншага мноства, то адзін круг адлюстроўваецца ўнутры іншага. Напрыклад, калі M  — мноства ўсіх драпежнікаў, а A — мноства ўсіх ільвоў (A  ⊂ M), то гэта абазначаецца так:

Мноствы, у тым ліку і бясконцыя, у няяўнай форме выкарыстоўваліся ў матэматыцы з часоў Старажытнай Грэцыі.
Да XIX ст. лічылася, што дакладнага азначэння мноства няма. Мноствам называлі любую сукупнасць, аб’яднанне прадметаў.

У канцы XIX ст. нямецкі матэматык Георг Кантар (1845—1918) вызначыў мноства як «адзінае імя для сукупнасці ўсіх аб’ектаў, якія валодаюць дадзенай уласцівасцю».

Паводле тэорыі Г. Кантара некаторыя мноствы канчатковыя (напрыклад, цэлыя лікі ад 1 да 7), а некаторыя — бясконцыя (напрыклад, цэлыя лікі). У некаторых выпадках элементы аднаго мноства строга адпавядаюць элементам іншага мноства, напрыклад мноства колераў вясёлкі і мноства цэлых лікаў ад 1 да 7.

Прыклад 5.1. Няхай M — мноства любімых вучэбных прадметаў сямікласніка Ігара, якое складаецца з элементаў: матэматыка, інфарматыка, англійская мова. Тады можна запісаць:

М = {матэматыка, інфарматыка, англійская мова};

інфарматыка ∈ М ;

літаратура ∉ М.

Прыклад 5.2. Няхай у мноства M уваходзяць усе вучэбныя прадметы, якія вывучаюцца ў 7-м класе. Пералічыць усе яго элементы можна, напрыклад, гледзячы на старонку школьнага дзённіка. Тады можна запісаць:

інфарматыка ∈ М ;

астраномія ∉ М .
Прыклад 5.3. Няхай М = {Вера, Сяргей, Вася, Віка, Ліза, Косця, Надзя} — мноства навучэнцаў 7 Б класа, якія займаюцца ў драмгуртку. З гэтага мноства можна вылучыць наступныя падмноствы:

А = {Вера, Віка, Ліза, Надзя} — мноства дзяўчынак (чырвоная мяжа).

В = {Сяргей, Вася, Косця} — мноства хлопчыкаў (сіняя мяжа).

С = {Вера, Вася, Віка} — мноства дзяцей, чые імёны пачынаюцца на літару «В» (зялёная мяжа).

D = {Вера, Сяргей, Вася, Віка, Ліза, Косця, Надзя} — мноства дзяцей, у імёнах якіх па 2 галосныя гукі (жоўтая мяжа).

E = ∅  — мноства трохгадовых дзяцей.

Леанард Эйлер (1707—1783) — вучоны, які ўнёс значны ўклад у развіццё матэматыкі і механікі, а таксама фізікі, астраноміі і шэрага прыкладных навук.
Распрацаваў зручны метад для графічнага адлюстравання адносін паміж мноствамі.


1 Што разумеюць пад мноствам?



2 Што разумеюць пад падмноствам?



3 Што выкарыстоўваецца для геаметрычнай ілюстрацыі мностваў?



  1. 1 Дапоўніце кожнае з мностваў 1—2 элементамі.
    1. А = {матэматыка, інфарматыка, гісторыя, літаратура};
    2. В = {яблык, груша, апельсін, банан};
    3. С = {клавіятура, манітор, мыш};
    4. D = {аловак, ручка, рызінка, фламастар}.

 

  1. 2 Якія элементы могуць уваходзіць у наступныя мноствы?
    1. Транспартныя сродкі.
    2. Колеры вясёлкі.
    3. Хатнія жывёлы.
    4. Цотныя лікі.

 

  1. 3 Адкрыйце файл з групамі слоў. Падзяліце словы кожнай групы на два мноствы. Словы першага мноства вылучыце чырвоным колерам, а другога — сінім. Па якіх прыметах вы падзялілі словы? Узор:
    1. Тэкст у файле: гусь, лебедзь, заяц, воўк, паўлін, курыца, дзік, лось.
    Вынік: А = {гусь, лебедзь, паўлін, курыца};

    B = {заяц, воўк, дзік, лось}.

    Прыметы: А — мноства птушак, В — мноства звяроў.
    2. Мяч, стол, крэсла, канькі, шафа, клюшка, шайба, камода.
    3. Сом, вуж, карась, акунь, шчупак, гадзюка, кобра, пітон.

 

  1. 4 З мноства геаметрычных фігур А = {круг, авал, квадрат, прамавугольнік, трохвугольнік, пяцівугольнік} вылучыце падмноствы:
    1. Фігур, што не маюць вуглоў.
    2. Фігур, што з’яўляюцца чатырохвугольнікамі.
    3. Фігур, колькасць вуглоў у якіх большая за тры.

 

  1. 5 Адкрыйце файл з рысункамі геаметрычных фігур. З дапамогай аперацыі капіравання стварыце падмноствы а, б, в, якія валодаюць прыметамі, названымі ў заданні 4. Усе элементы кожнага падмноства змясціце ўнутры адпаведнага прамавугольніка.
  2. 6 Адкрыйце файл з рысункамі матылькоў. Выкарыстоўваючы аперацыю капіравання, стварыце ніжэйпералічаныя падмноствы і змясціце іх у прамавугольніках.

    1. Матылькі, у афарбоўцы якіх ёсць сіні колер.
    2. Матылькі, у афарбоўцы якіх ёсць чырвоны колер.
    3. Матылькі, у афарбоўцы якіх ёсць зялёны колер.
    4. Матылькі, у афарбоўцы якіх ёсць жоўты колер.

 

  1. 7 Зададзены два мноствы: K — мноства кніг у школьнай бібліятэцы; U — мноства вучэбных дапаможнікаў у гэтай жа бібліятэцы. Якое з мностваў з’яўляецца падмноствам іншага? Адлюструйце іх з дапамогай кругоў Эйлера.