12.1. Каманда галінавання

Даволі часта на пастаўленае пытанне чалавек атрымлівае адказ «Так» або «Не». У залежнасці ад адказу ён вызначае свае дзеянні і выконвае адну ці другую каманду (групу каманд).

Робаты і іншыя тэхнічныя ўстройствы таксама могуць выконваць розныя дзеянні ў залежнасці ад умовы. Калі ўмова праўдзівая (на пытанне атрыманы адказ «Так»), то выконваюцца адны дзеянні, калі непраўдзівая, то іншыя.

Алгарытмічная канструкцыя галінаванне забяспечвае выкананне адной ці другой паслядоўнасці каманд у залежнасці ад праўдзівасці або непраўдзівасці некаторай умовы.

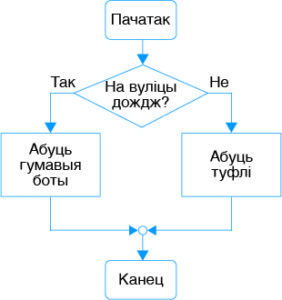
Галінаванне можа адлюстроўвацца на блок-схеме такім чынам:

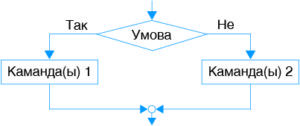
У дадзенай канструкцыі ў пра-мавугольніку(-ах) запісваюцца каманды алгарытму. Пры такой арганізацыі алгарытму можа выканацца толькі адна з дзвюх каманд (паслядоўнасцей каманд). Іншая паслядоўнасць будзе праігнаравана (пример 12.1).

Для запісу канструкцыі галінавання ў мове праграміравання Pascal выкарыстоўваецца каманда if. Фfрмат запiсу каманды:

if <умова> then

begin

каманды 1;

end

else

begin

каманды 2;

end;

Радок if <умова> then з’яўляецца загалоўкам галінавання. Гэты радок можна прачытаць так: «Калі ўмова правільная, то». Пасля слова then запісваецца паслядоўнасць каманд 1, якая выканаецца, калі ўмова праўдзівая. Пасля слова else запісваецца паслядоўнасць каманд 2, якая выканаецца, калі ўмова непраўдзівая. Словы begin и end; у дадзеным выпадку адыгрываюць ролю аператарных дужак. Звярніце ўвагу, што перад словам else кропка з коскай не ставіцца.

Галінаванне можа быць запісана ў поўнай або скарочанай форме.

Поўная форма галінавання прадугледжвае арганізацыю выканання двух розных набораў каманд, з якіх выконваецца толькі адзін. У скарочанай форме адзін з набораў каманд (часцей па адказе «Не») прапускаецца. У гэтым выпадку, калі ўмова непраўдзівая, то ніякія дзеянні не выконваюцца.

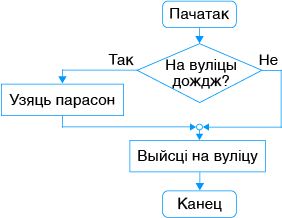
Блок-схема скарочанай формы галінавання:

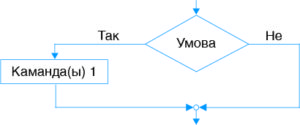
(Разгледзьце прыклад 12.2.)

На мове праграміравання Pascal каманда запішацца так:

if <умова> then

begin

каманды 1;

end;

Алгарытм можа змяшчаць больш за адну канструкцыю галінавання (прыклад 12.3).

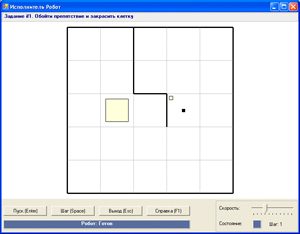
Прыклад 12.4. Рэшым задачу if1 з убудаванага задачніка.

Робат павінен зафарбаваць клетку, якая знаходзіцца за сцяной. У залежнасці ад становішча абход сцяны можа ажыццяўляцца па-рознаму.

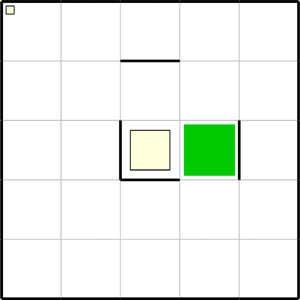
Спачатку Робат павінен зрушыцца ўправа. Калі сцяна знізу, то зверху свабодна і можна абысці сцяну зверху, у адваротным выпадку Робат абыходзіць сцяну знізу.

Пасля абходу сцяны Робат зафарбоўвае клетку. Алгарытм можна запісаць так:

управа;
Калі зверху свабодна, то
ўверх; управа; уніз;
Інакш
уніз; управа; уверх;
зафарбаваць.

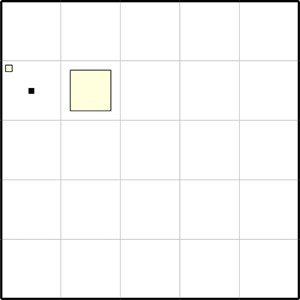
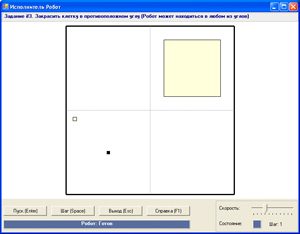
Прыклад 12.5. Робат знаходзіцца на невядомай клетцы поля без ліній. Ён павінен зафарбаваць клетку злева ад сябе.

Для таго каб зафарбаваць клетку злева ад сябе, Робат павінен перамясціцца ўлева, а затым зафарбаваць клетку. Аднак зрабіць гэта Робат зможа толькі тады, калі не знаходзіцца ў клетках, якія з’яўляюцца левай мяжой поля. Таму, перш чым зрушыцца ўлева, Робат павінен праверыць, ці свабодна злева.

Вынік работы дадзенай праграмы залежыць ад пачатковага становішча Робата. Таму для праверкі правільнасці работы праграмы неабходна падрыхта-
ваць пачатковыя становішчы, якія даюць розныя адказы на пытанне: злева пуста?

12.2. Састаўныя ўмовы

У якасці ўмовы ў алгарытмах з цыкламі і галінаваннямі выкарыстоўваецца любое зразумелае выканаўцы гэтага алгарытму выказванне, якое можа быць або праўдзівым, або непраўдзівым.

Усе ўмовы, з якімі нам даводзілася дагэтуль сустракацца пры складанні алгарытмаў для Робата, былі простымі выказваннямі. Аднак можна будаваць і састаўныя ўмовы.

Састаўная ўмова — умова, якая ўтвараецца з некалькіх простых умоў, злучаных адна з адной лагічнымі аперацыямі.

З лагічнымі аперацыямі над выказваннямі вы ўжо знаёмыя. У PascalABC выкарыстоўваюцца наступныя лагічныя аперацыі:

Лагічная аперацыя	Запіс у PascalABC
Не	Not
I	And
Або	Or

(Разгледзьце прыклад 12.6.)

Сістэма ўмоў для Робата пабудавана так, што можна абысціся без выкарыстання лагічнай аперацыі адмаўлення.

Для ўмовы FreeFromLeft адмаўленнем будзе ўмова not FreeFromLeft. Але ўмова «злева не свабодна» азначае, што там сцяна. Таму замест умовы not FreeFromLeft можна пісаць WallFromLeft. Адмаўленні іншых умоў паказаны ў табліцы:

Умова	Адмаўленне
WallFromLeft	FreeFromLeft
WallFromRight	FreeFromRight
WallFromUp	FreeFromUp
WallFromDown	FreeFromDown
CellIsPainted	CellIsFree

Паняцце галінавання выкарыстоўваецца ў розных сферах чалавечай дзейнасці. У батаніцы пад галінаваннем парасткаў разумеюць працэс утварэння бакавых парасткаў у раслін. Пры ўжыванні тэрміна ў пераносным сэнсе пад галінаваннем разумеюць наяўнасць некалькіх шляхоў, напрамкаў, сюжэтных ліній і г. д. Галінаванні выкарыстоўваюцца ў дарожнай разметцы і картаграфіі.

Прыклад 12.1. Выбар абутку вясной у залежнасці ад надвор’я: Калі на вуліцы дождж, то          абуць гумавыя боты; Інакш          абуць туфлі У дадзеным прыкладзе ў цяперашні момант часу можа быць выканана толькі адна каманда з дзвюх: або абуць боты, або абуць туфлі. Блок-схема дадзенага алгарытму будзе выглядаць наступным чынам: Прыклад 12.2. Выхад на вуліцу восенню. Калі на вуліцы дождж, то            ўзяць парасон; выйсці на вуліцу. Тут выкарыстоўваецца скарочаная форма каманды галінавання. Калі ўмова праўдзівая, выконваецца каманда «ўзяць парасон». Калі ўмова непраўдзівая, ніякіх дзеянняў не адбываецца. Каманда «выйсці на вуліцу» выконваецца заўсёды. Блок-схема алгарытму: Прыклад 12.3. Маецца тры манеты, сярод якіх адна фальшывая. Фальшывая манета лягчэйшая за сапраўдныя. Знойдзем фальшывую манету за мінімальны лік узважванняў на шалях без гір: Пакласці на кожную шалю манеты 1 і 2; Калі шалі ўраўнаважаны, то       фальшывая манета 3; Інакш      Калі     манета     1     цяжэйшая,     то                 фальшывая манета 2;      Інакш                 фальшывая манета 1. Прыклад 12.4. Магчымыя пачатковыя становішчы: Праграма для Робата: Delphi/Pascal uses Robot; begin Task('if1'); right; if FreeFromUp then begin up; right; down; end else begin down; right; up; end; paint; end. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 uses Robot; begin Task('if1'); right; if FreeFromUp then begin up; right; down; end else begin down; right; up; end; paint; end. Прыклад 12.5. Праграма для выканаўцы Робат: Delphi/Pascal uses Robot, RobTasks; begin Task(‘myrob9’); If FreeFromLeft then begin left; paint; end; end. 1 2 3 4 5 6 7 8 uses Robot, RobTasks; begin Task(‘myrob9’); If FreeFromLeft then begin left; paint; end; end. 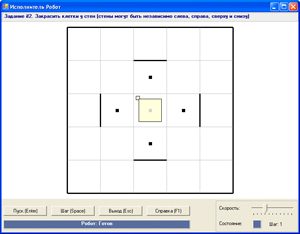Магчымыя пачатковыя становішчы: Прыклад 12.6. Разгледзім наступнае пачатковае становішча поля для выканаўцы Робат: Праверым для Робата наступныя састаўныя ўмовы: 1. WallFromLeft and CellIsPainted. 2. WallFromUp or WallFromDown. 3. Not (WallFromRight or FreeFromUp). Першая ўмова складаецца з дзвюх простых: WallFromLeft (умова А) і CellIsPainted (умова В). Умова можа быць запісана як «А І В». Гэта ўмова правільная толькі тады, калі правільныя і А, і В. Умова А — WallFromLeft — праўдзівая, умова В — CellIsPainted — праўдзівая, умова А І В — праўдзівая. Другая ўмова можа быць запісана як «А АБО В», дзе А — WallFromUp, В — WallFromDown. Умова А — праўдзівая, умова В — непраўдзівая. Значыць, умова «А АБО В» — праўдзівая. У трэцяй умове часціца not адмаўляе састаўную ўмову WallFromRight or FreeFromUp. Умова можа быць запісана як НЕ (А АБО В). Для таго каб вызначыць, праўдзівая ці непраўдзівая гэта ўмова, трэба спачатку вызначыць праўдзівасць умовы «А АБО В». Умова А — непраўдзівая, умова В таксама непраўдзівая. Таму непраўдзівай будзе і ўмова «А АБО В», але тады ўмова НЕ (А АБО В) будзе праўдзівай.

---

Тэсты Практыкаванні

---