[:ru]
5.1. Понятие множества
Рассмотрим высказывание «Все учащиеся нашего класса имеют дома компьютер». Истинно оно или ложно? Для ответа на этот вопрос вам нужно задать каждому из одноклассников вопрос: «У тебя дома есть компьютер?» Если все учащиеся класса ответят утвердительно, то высказывание истинно, если хотя бы один из учащихся ответит «нет», то и высказывание будет ложным. Для разных классов это высказывание будет иметь различные значения, потому что различными будут множества учащихся класса.
Множество — совокупность каких-либо объектов, обладающих общим свойством. Эти объекты называют элементами множества.
Можно говорить о множестве учащихся 7 А класса, множестве отметок в классном журнале, множестве городов Беларуси, множестве букв русского алфавита и т. д. Понятие множества является одним из основных в математике.
Множества, как правило, обозначают прописными латинскими буквами, а элементы множества — строчными. Напомним, что для обозначения принадлежности элемента множеству используют специальные знаки:
а ∈ М (элемент а принадлежит множеству М), а ∉ М (элемент а не принадлежит множеству М). Если множество M состоит из элементов a, b, c, то это записывают так: M = {a, b, c}.
Чтобы задать множество, необходимо перечислить его элементы (пример 5.1) или назвать их общее свойство (пример 5.2).
5.2. Понятие подмножества
Рассмотрим множество учащихся какого-либо класса. В этом множестве можно выделить не только отдельного учащегося, но и некоторые группы учащихся. Например, отличники, учащиеся, умеющие играть в теннис, изучающие французский язык и т. д. Каждая из таких групп образует подмножество — часть множества учащихся.
Если множество А является подмножеством множества М, то это записывают так:
А ⊂ М. Запись А ⊄ М обозначает, что множество А не является подмножеством множества М.
Подмножество может содержать все элементы множества, а может не содержать ни одного (пустое множество; обозначается знаком ∅).
Некоторые элементы множества могут принадлежать одновременно разным подмножествам (пример 5.3).
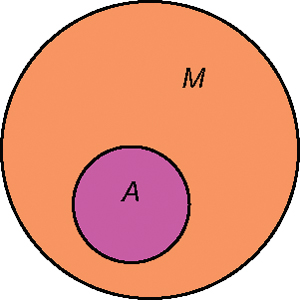
Для наглядной геометрической иллюстрации множеств и отношений между ними используют круги Эйлера. Каждое множество изображается кругом. Если какое-либо множество является подмножеством другого множества, то один круг изображается внутри другого. Например, если M — множество всех хищников, а A — множество всех львов (A ⊂ M), то это обозначается таким образом:
|
Множества, в том числе и бесконечные, в неявной форме использовались в математике со времен Древней Греции. До XIX в. считалось, что точного определения множества нет. Множеством называли любое скопление, объединение предметов.
В конце XIX в. немецкий математик Георг Кантор (1845—1918) определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Пример 5.1. Пусть множество M — это множество любимых учебных предметов семиклассника Игоря, состоящее из следующих элементов: математика, информатика, английский язык. Тогда можно записать: М = {математика, информатика, английский язык}; информатика ∈ М ; литература ∉ М. Пример 5.2. Пусть в множество M входят все учебные предметы, которые изучаются в 7-м классе. Перечислить все элементы данного множества можно, например, глядя на страницу школьного дневника. Тогда можно записать: информатика ∈ М ; астрономия ∉ М . |
|
Пример 5.3. Пусть М = {Вера, Сергей, Вася, Вика, Лиза, Костя, Надя} — множество учащихся 7 Б класса, занимающихся в драмкружке. Из этого множества можно выделить следующие подмножества:
А = {Вера, Вика, Лиза, Надя} — множество девочек (красная граница). В = {Сергей, Вася, Костя} — множество мальчиков (синяя граница). С = {Вера, Вася, Вика} — множество детей, чьи имена начинаются на букву «В» (зеленая граница). D = {Вера, Сергей, Вася, Вика, Лиза, Костя, Надя} — множество детей, в именах которых по 2 гласных звука (желтая граница). E = ∅ — множество трехлетних детей. |
|
Леонард Эйлер (1707—1783) — ученый, внесший значительный вклад в развитие математики и механики, а также физики, астрономии и ряда прикладных наук. |
[:ru]1 Что понимают под множеством?[:by]1 Што разумеюць пад мноствам?[:]
2. Что понимают под подмножеством?
3. Что используется для геометрической иллюстрации множеств?
- 1 Дополните каждое из множеств 1—2 элементами.
1. А = {математика, информатика, история, литература};
2. В = {яблоко, груша, апельсин, банан};
3. С = {клавиатура, монитор, мышь};
4. D = {карандаш, ручка, ластик, фломастер}.
- 2 Какие элементы могут входить в следующие множества?
1. Средства передвижения;
2. цвета радуги;
3. домашние животные;
4. четные числа.
- 3 Откройте файл с группами слов. Разделите слова каждой группы на два множества. Слова первого множества выделите красным цветом, а второго — синим. По каким признакам вы разделили слова? Образец:
1. Текст в файле: гусь, лебедь, заяц, волк, павлин, курица, кабан, лось.
Результат: А = {гусь, лебедь, павлин, курица};B = {заяц, волк, кабан, лось}.
Признаки: А — множество птиц, В — множество зверей;
2. мяч, стол, стул, коньки, шкаф, клюшка, шайба, комод;
3. сом, уж, карась, окунь, щука, гадюка, кобра, питон.
- 4 Из множества геометрических фигур А = {круг, овал, квадрат, прямоугольник, треугольник, пятиугольник} выделите подмножества:
1) фигур, не имеющих углов;
2) фигур, являющихся четырехугольниками;
3) фигур, количество углов у которых больше трех.
- 5 Откройте файл с изображениями геометрических фигур. С помощью операции копирования создайте подмножества а, б, в. Все элементы каждого подмножества разместите внутри соответствующего прямоугольника.
- 6 Откройте файл с изображением бабочек. Используя операцию копирования, создайте нижеперечисленные подмножества и разместите их в прямоугольниках.
1. Бабочки, в раскраске которых есть синий цвет;
2. бабочки, в раскраске которых есть красный цвет;
3. бабочки, в раскраске которых есть зеленый цвет;
4. бабочки, в раскраске которых есть желтый цвет.- 7 Заданы два множества: K — множество книг в школьной библиотеке; U — множество учебных пособий в этой же библиотеке. Какое из множеств является подмножеством другого? Изобразите их с помощью кругов Эйлера.
[:by]
5.1. Паняцце мноства
Разгледзім выказванне «Усе навучэнцы нашага класа маюць дома камп’ютар». Праўдзівае яно ці непраўдзівае? Для адказу на гэта пытанне вам трэба ў кожнага з аднакласнікаў удакладніць: «У цябе дома ёсць камп’ютар?» Калі ўсе навучэнцы класа адкажуць сцвярджальна, то выказванне праўдзівае, калі хоць бы адзін з навучэнцаў адкажа «няма»,
то і выказванне будзе непраўдзівым. Для розных класаў гэта выказванне будзе мець розныя значэнні, таму што рознымі будуць мноствы навучэнцаў класа.
Мноства — сукупнасць якіх-небудзь аб’ектаў, што валодаюць агульнай уласцівасцю. Гэтыя аб’екты называюць элементамі мноства.
Можна гаварыць пра мноства навучэнцаў 7 А класа, мноства адзнак у класным журнале, мноства гарадоў Беларусі, мноства літар рускага алфавіта і г. д. Паняцце мноства з’яўляецца адным з асноўных у матэматыцы.
Мноствы, як правіла, абазначаюць вялікімі лацінскімі літарамі, а элементы мностваў — маленькімі. Нагадаем, што для абазначэння прыналежнасці элемента мноству выкарыстоўваюць спецыяльныя знакі:
а ∈ М (элемент а належыць мноству М), а ∉ М (элемент а не належыць мноству М). Калі мноства M складаецца з элементаў a, b, c, то гэта запісваюць так: M = {a, b, c}.
Каб задаць мноства, неабходна пералічыць яго элементы (прыклад 5.1) або назваць іх агульную ўласцівасць (прыклад 5.2).
5.2. Паняцце падмноства
Разгледзім мноства навучэнцаў якога-небудзь класа. У гэтым мностве можна вылучыць не толькі асобнага навучэнца, але і некаторыя групы навучэнцаў: выдатнікі; навучэнцы, што ўмеюць гуляць у тэніс, і г. д. Кожная з такіх груп утварае падмноства — частку мноства навучэнцаў.
Калі мноства А з’яўляецца падмноствам мноства М, то гэта запісваюць так: А ⊂ М. Запіс А ⊄ М абазначае, што мноства А не з’яўляецца падмноствам мноства М.
Падмноства можа змяшчаць усе элементы мноства, а можа не змяшчаць ніводнага (пустое мноства абазначаецца знакам ∅).
Некаторыя элементы мноства могуць належаць адначасова розным падмноствам (прыклад 5.3).
Для нагляднай геаметрычнай ілюстрацыі мностваў і адносін паміж імі выкарыстоўваюць кругі Эйлера. Кожнае мноства адлюстроўваецца кругам. Калі якое-небудзь мноства з’яўляецца падмноствам іншага мноства, то адзін круг адлюстроўваецца ўнутры іншага. Напрыклад, калі M — мноства ўсіх драпежнікаў, а A — мноства ўсіх ільвоў (A ⊂ M), то гэта абазначаецца так:
| Мноствы, у тым ліку і бясконцыя, у няяўнай форме выкарыстоўваліся ў матэматыцы з часоў Старажытнай Грэцыі. Да XIX ст. лічылася, што дакладнага азначэння мноства няма. Мноствам называлі любую сукупнасць, аб’яднанне прадметаў.
У канцы XIX ст. нямецкі матэматык Георг Кантар (1845—1918) вызначыў мноства як «адзінае імя для сукупнасці ўсіх аб’ектаў, якія валодаюць дадзенай уласцівасцю». Паводле тэорыі Г. Кантара некаторыя мноствы канчатковыя (напрыклад, цэлыя лікі ад 1 да 7), а некаторыя — бясконцыя (напрыклад, цэлыя лікі). У некаторых выпадках элементы аднаго мноства строга адпавядаюць элементам іншага мноства, напрыклад мноства колераў вясёлкі і мноства цэлых лікаў ад 1 да 7. Прыклад 5.1. Няхай M — мноства любімых вучэбных прадметаў сямікласніка Ігара, якое складаецца з элементаў: матэматыка, інфарматыка, англійская мова. Тады можна запісаць: М = {матэматыка, інфарматыка, англійская мова}; інфарматыка ∈ М ; літаратура ∉ М. Прыклад 5.2. Няхай у мноства M уваходзяць усе вучэбныя прадметы, якія вывучаюцца ў 7-м класе. Пералічыць усе яго элементы можна, напрыклад, гледзячы на старонку школьнага дзённіка. Тады можна запісаць: інфарматыка ∈ М ; астраномія ∉ М . |
| Прыклад 5.3. Няхай М = {Вера, Сяргей, Вася, Віка, Ліза, Косця, Надзя} — мноства навучэнцаў 7 Б класа, якія займаюцца ў драмгуртку. З гэтага мноства можна вылучыць наступныя падмноствы:
А = {Вера, Віка, Ліза, Надзя} — мноства дзяўчынак (чырвоная мяжа). В = {Сяргей, Вася, Косця} — мноства хлопчыкаў (сіняя мяжа). С = {Вера, Вася, Віка} — мноства дзяцей, чые імёны пачынаюцца на літару «В» (зялёная мяжа). D = {Вера, Сяргей, Вася, Віка, Ліза, Косця, Надзя} — мноства дзяцей, у імёнах якіх па 2 галосныя гукі (жоўтая мяжа). E = ∅ — мноства трохгадовых дзяцей. |
|
Леанард Эйлер (1707—1783) — вучоны, які ўнёс значны ўклад у развіццё матэматыкі і механікі, а таксама фізікі, астраноміі і шэрага прыкладных навук. |
[:ru]1 Что понимают под множеством?[:by]1 Што разумеюць пад мноствам?[:]
2. Что понимают под подмножеством?
3. Что используется для геометрической иллюстрации множеств?
- 1 Дапоўніце кожнае з мностваў 1—2 элементамі.
1. А = {матэматыка, інфарматыка, гісторыя, літаратура};
2. В = {яблык, груша, апельсін, банан};
3. С = {клавіятура, манітор, мыш};
4. D = {аловак, ручка, рызінка, фламастар}.
- 2 Якія элементы могуць уваходзіць у наступныя мноствы?
1. Транспартныя сродкі.
2. Колеры вясёлкі.
3. Хатнія жывёлы.
4. Цотныя лікі.
- 3 Адкрыйце файл з групамі слоў. Падзяліце словы кожнай групы на два мноствы. Словы першага мноства вылучыце чырвоным колерам, а другога — сінім. Па якіх прыметах вы падзялілі словы? Узор:
1. Тэкст у файле: гусь, лебедзь, заяц, воўк, паўлін, курыца, дзік, лось.
Вынік: А = {гусь, лебедзь, паўлін, курыца};B = {заяц, воўк, дзік, лось}.
Прыметы: А — мноства птушак, В — мноства звяроў.
2. Мяч, стол, крэсла, канькі, шафа, клюшка, шайба, камода.
3. Сом, вуж, карась, акунь, шчупак, гадзюка, кобра, пітон.
- 4 З мноства геаметрычных фігур А = {круг, авал, квадрат, прамавугольнік, трохвугольнік, пяцівугольнік} вылучыце падмноствы:
1. Фігур, што не маюць вуглоў.
2. Фігур, што з’яўляюцца чатырохвугольнікамі.
3. Фігур, колькасць вуглоў у якіх большая за тры.
- 5 Адкрыйце файл з рысункамі геаметрычных фігур. З дапамогай аперацыі капіравання стварыце падмноствы а, б, в, якія валодаюць прыметамі, названымі ў заданні 4. Усе элементы кожнага падмноства змясціце ўнутры адпаведнага прамавугольніка.
- 6 Адкрыйце файл з рысункамі матылькоў. Выкарыстоўваючы аперацыю капіравання, стварыце ніжэйпералічаныя падмноствы і змясціце іх у прамавугольніках.
1. Матылькі, у афарбоўцы якіх ёсць сіні колер.
2. Матылькі, у афарбоўцы якіх ёсць чырвоны колер.
3. Матылькі, у афарбоўцы якіх ёсць зялёны колер.
4. Матылькі, у афарбоўцы якіх ёсць жоўты колер.
- 7 Зададзены два мноствы: K — мноства кніг у школьнай бібліятэцы; U — мноства вучэбных дапаможнікаў у гэтай жа бібліятэцы. Якое з мностваў з’яўляецца падмноствам іншага? Адлюструйце іх з дапамогай кругоў Эйлера.
[:]